如何高效指导学生进行数学建模？关键方法与技巧全解析

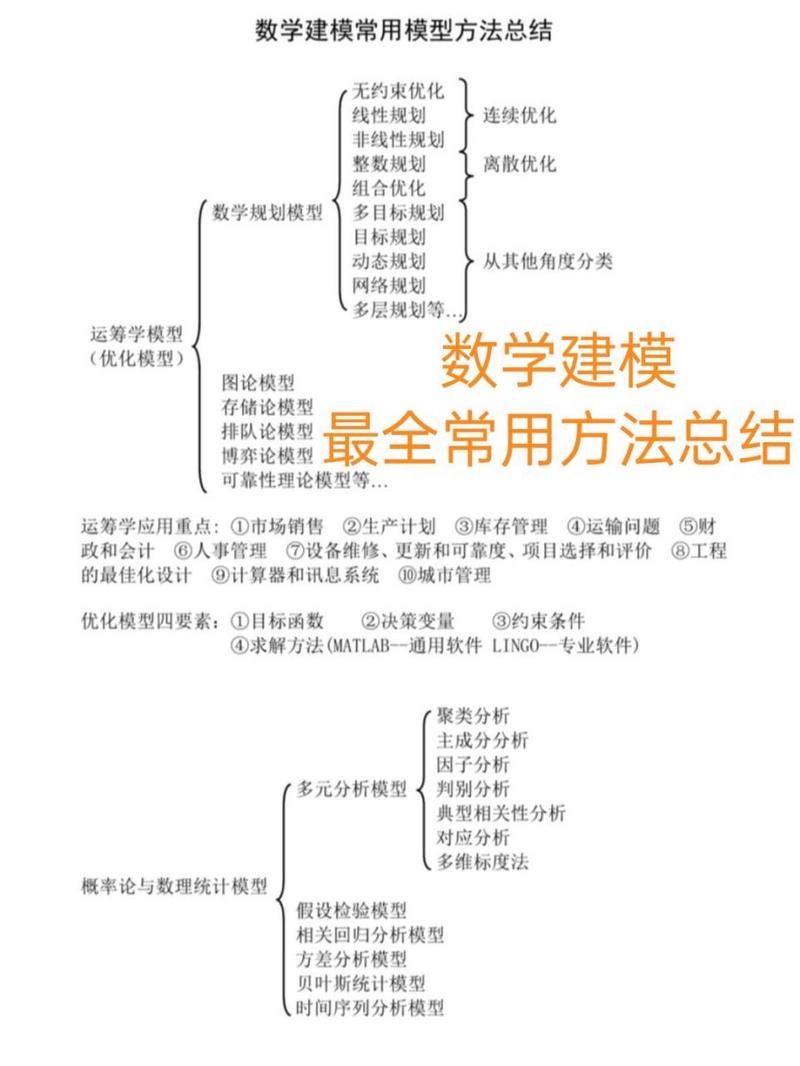
数学建模是连接理论与实际问题的桥梁,对学生综合能力要求极高，作为指导过多次建模竞赛的教师，我认为掌握核心方法比盲目刷题更重要，以下是基于实战经验的指导建议，适用于入门到进阶不同阶段的学生。

培养问题拆解思维时，先画出“问题树”：用分层结构分解核心问题，例如研究城市交通拥堵，可分为道路设计、车流量、信号灯控制等分支，每个子问题对应特定数学模型，去年国赛A题获奖团队正是用这种方法，将卫星定位误差拆分为时钟偏差、大气延迟等6个维度分别建模。

数据处理的三个陷阱

1. 不要直接使用原始数据,去年美赛某队伍因未处理传感器采集的温度异常值，导致预测模型误差扩大37%
2. 特征工程决定上限,建议先用皮尔逊系数筛选相关度>0.6的变量
3. 时间序列必须检验平稳性,差分处理次数不要超过2次，否则会损失原始信息

模型选择的两大准则 优先考虑可解释性强的模型，如微分方程、线性规划，某次电力调度问题中，灰色预测模型比神经网络更容易被评委认可，当预测精度更重要时，可尝试XGBoost与LSTM融合模型，去年深交所金融挑战赛冠军团队用此方法将预测误差降至1.8%。

验证环节常被忽视的细节

1. 交叉验证要分层抽样,特别是处理医疗数据时保持患者年龄分布一致
2. 灵敏度分析要做参数扰动实验,变化幅度建议设为±15%
3. 可视化必须包含误差带,折线图比柱状图更能体现趋势变化

写作的黄金结构 引言用“问题场景+现有研究缺陷”开头，方法部分插入流程图，结果展示采用对比表格，特别注意变量符号必须全篇统一，去年有23%的参赛论文因符号混乱被扣分，附录放核心代码片段，但需删除调试用的print语句。

数学建模的本质是系统化解决问题的训练,遇到过凌晨三点还在调试参数的学生，也见过因变量单位错误导致全盘重算的案例，这些经历印证了一个道理：优秀模型往往诞生于对细节的执着，建议每周做1次限时建模训练，把查文献、编程、写作的全流程压缩在6小时内完成，当你能从容应对各种突发状况时，离拿奖就不远了。