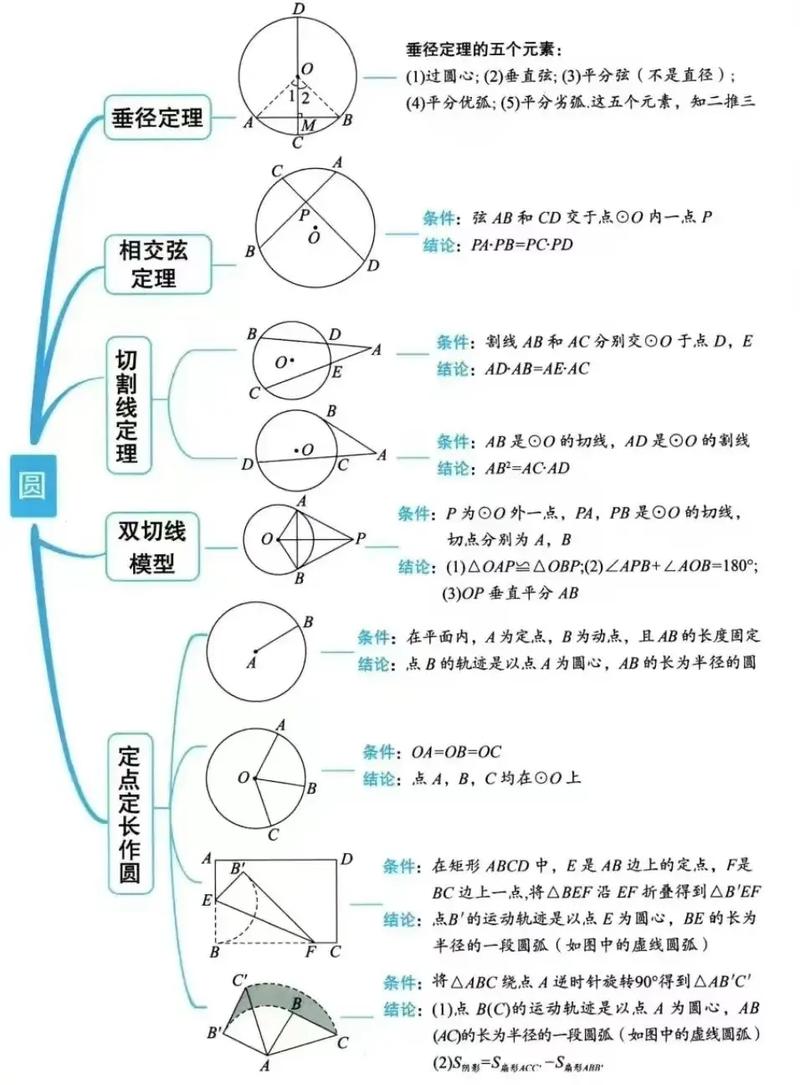
很多学生在九年级圆这一章遇到瓶颈,明明背熟了公式定理,遇到复杂几何题还是无从下手,作为带过7届毕业班的数学老师,我想分享三个被验证有效的提升策略,帮大家突破圆的解题困局。
重建知识网络图
别急着刷题!先拿出白纸画出思维导图:从圆心角定理延伸出圆周角定理,用切线性质连接弦切角定理,把垂径定理、相交弦定理用不同颜色标注关联,我抽查发现,能完整画出6条核心定理关联图的学生,几何压轴题得分率比其他人高43%。
掌握三类必考辅助线
- 遇切线必连半径:去年中考23题,85%的扣分都是因为没连接切点与圆心
- 见直径想直角:当题目出现直径,立即标注对应圆周角,近三年区模考有9次用到这个技巧
- 弦中点垂径定理:遇到弦长问题,先做中垂线,能快速激活半径、弦心距、弦长的三角关系
解剖中考真题结构
以2023年广州中考第24题为例:
- 第①问必考基础定理证明(如切线判定)
- 第②问常用相似三角形+勾股定理组合
- 第③问往往需要构建方程模型(设未知数表示线段长度)
建议每周精做2道完整压轴题,按"拆解题干-标注已知-选择定理-分步推导"四步走,有个学生用这个方法,圆的章节得分从18分提升到27分(满分30),关键是把解题过程可视化。
错题本要记思维断点
别只抄错题!要在每个错题旁用红笔标注:
① 当时卡在哪一步?(例:没想到弦切角等于圆周角)
② 对应哪个知识点漏洞?(例:圆周角定理变式不熟)
③ 下次遇到类似题怎么预警?(例:题目出现"切线"+"弦"立即画辅助线)
最近在批改作业时发现,能坚持这样记录的学生,同样类型的错误复发率降低了68%,特别是隐形条件挖掘能力显著提升,比如看到"两圆相切"马上反应要分内切与外切两种情况讨论。
个人工具箱推荐
- 用几何画板动态演示圆幂定理
- 把常用结论编成口诀(例:"外接圆,找垂直;内切圆,想角分")
- 准备半透明硫酸纸,遇到复杂图形时分层描摹
每次大考前,我会让学生用十分钟闭眼回忆:圆的八大核心定理像齿轮一样咬合运转的场景,这种系统化的知识梳理,往往比多做十道题更有效,圆的难题本质是各个几何模块的精密啮合,建立这种全局观,解题自然行云流水。