第一步:确定圆心与半径
用圆规画任意大小圆形,标记圆心点O,圆心是后续所有等分操作的基准点,必须清晰明确,保持半径不变,避免后续步骤出现比例错误。
第二步:计算等分角度
数学原理:圆周角为360°,等分n份时,每份对应圆心角θ=360°/n。
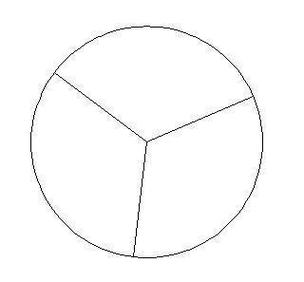
- 三等分:θ=120°
- 六等分:θ=60°
若需高精度,用量角器直接测量;若徒手操作,可用直尺辅助估算角度。
第三步:标记等分点
- 从圆心出发,沿水平方向画一条半径OA;
- 以OA为基准线,顺时针或逆时针旋转θ角,标记点B;
- 重复旋转并标记,直到回到起点,形成闭合的n个等分点。
关键技巧:
- 对称验证:对偶数等分(如4、6、8),可通过画垂直直径快速定位对称点;
- 正多边形性质:连接相邻等分点可得到正n边形,边长相等的特性可反向验证等分是否准确。
第四步:连接与扩展应用
- 基础连线:直接连接相邻等分点,形成正多边形轮廓;
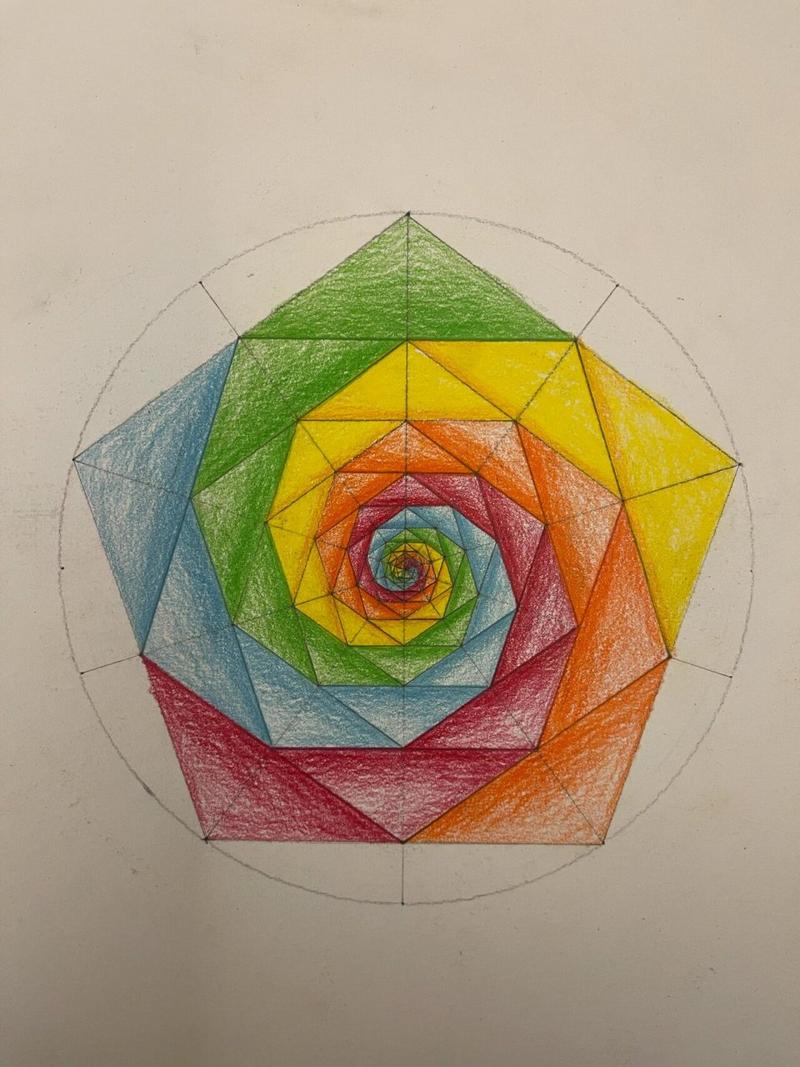
- 复杂图案:间隔连接等分点(如隔1点连成五角星),或叠加不同等分数(如3等分+4等分)创造对称花纹;
- 误差修正:若连线后图形不对称,需重新检查圆心位置或角度计算。
数学本质:全等与对称
等分圆的核心是构造全等的圆心角,几何学中,正多边形的每个边对应相同的弦长与圆心角,这一性质确保了等分的绝对均匀性,从三角函数角度,弦长公式c=2r·sin(θ/2)揭示了半径与等分数之间的定量关系。
课堂常见问题
- “不用量角器如何等分?”
利用直尺与圆规的经典几何法:例如六等分可通过半径截取法实现,因正六边形边长等于半径;
- “等分后线条不重合怎么办?”
检查圆心是否偏移,或圆规半径在操作中松动;
- “如何快速教学生理解抽象角度?”
将圆形类比钟表盘,用12小时刻度具象化30°等分概念。
个人观点
许多学生认为“等分圆”只是机械操作,实则每一步都渗透着几何的确定性美感,尝试闭眼想象:当n趋近无穷大,等分点连成的正多边形将无限接近完美的圆——这恰是微积分中“以直代曲”思想的启蒙,动手画图时,不妨多问“为什么必须从圆心出发”,答案就藏在圆作为“所有点到中心距离相等”的本质定义中。