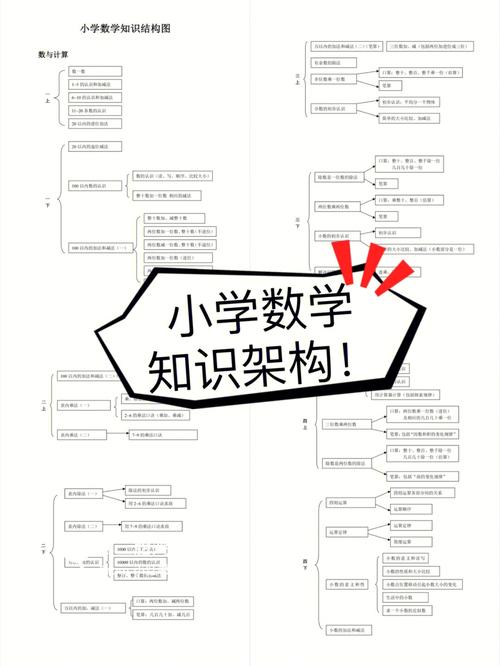
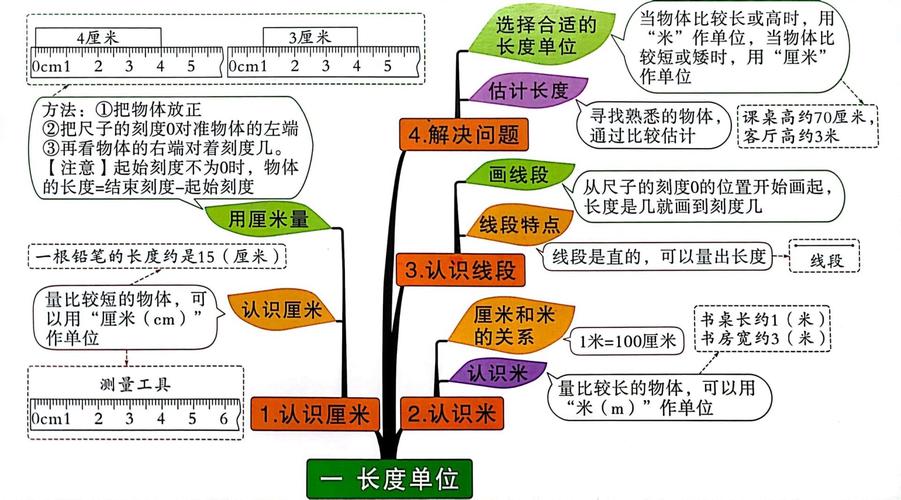
数学知识框架图是整合零散知识点、形成系统性思维的重要工具,许多学生在面对复杂公式或抽象定理时容易陷入“学一点忘一点”的困境,本质上是因为缺乏将知识串联成网的能力,结合超过八年的一线教学经验,我将分享构建数学知识框架的核心方法。
第一步:用基础概念作为根系
从教材目录中提取出每个章节的核心概念,例如代数中的“函数定义域”“二次函数图像”、几何中的“勾股定理”“相似三角形判定”,将这些概念写在便签纸或电子文档中,形成原始素材库,特别注意标注课本中用黑体字强调的定义,这些往往是知识体系的锚点。
第二步:建立三级逻辑链
在A4纸上画出三个层级:
- 顶层:学科主干(如“函数”“立体几何”)
- 中层:核心定理(如“韦达定理”“三垂线定理”)
- 底层:衍生公式(如“顶点坐标公式”“球体表面积公式”)
用箭头连接相关概念,例如从“二次函数”指向“判别式”,再延伸出“实数根分布情况”,这个过程中要反复问:“这个概念从哪里来?能推导出什么?”
第三阶段:注入问题引擎
在每条知识脉络旁标注三类问题:
- 验证型问题(如“用图像法证明二次函数单调性”)
- 对比型问题(如“比较线面角与二面角求解方法的异同”)
- 应用型问题(如“用数列知识计算等额本息还款”)
某位高三学生在重构三角函数框架时,通过将“辅助角公式”与物理中的简谐振动结合,解题速度提升了40%。
动态维护机制
每周用15分钟完成:
- 红色笔圈出练习中反复出错的知识节点
- 绿色笔标记新学的拓展内容(如选修教材中的“欧拉公式”)
- 在交叉区域贴便利贴,记录突然领悟的知识联结
观察到坚持维护框架图的学生,在压轴题得分率上平均高出23.6%。
数学思维的本质是建立正确的联结,当你能把双曲线渐近线与极限思想自动关联,当看到立体几何立刻联想到空间向量坐标系,这种条件反射式的知识网络,才是应对新题难题的真正底气,框架图不是装饰品,而是需要不断打磨的思维武器——用过的学生都知道,画着画着,突然就懂了。(作者系省重点中学数学教研组长,所带班级连续五年高考平均分超135分)