初中数学中分解质因数的具体步骤是什么？

明确基本概念

1. 质数：大于1的自然数，只能被1和它本身整除（如2、3、5、7）。
2. 质因数：一个数的因数中，属于质数的部分，6的因数是1、2、3、6，其中质因数为2和3。

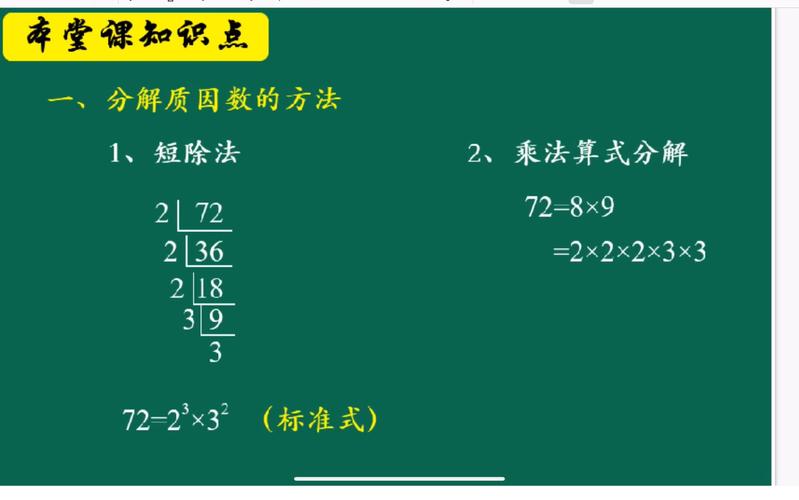
分解质因数的标准步骤
以数字60为例：

1. 从最小的质数开始试除：
   • 60 ÷ 2 = 30
   • 30 ÷ 2 = 15（无法继续用2除时，换下一个质数）
   • 15 ÷ 3 = 5
   • 5 ÷ 5 = 1（结果为1时停止）
2. 记录所有质因数：60 = 2 × 2 × 3 × 5
3. 合并指数形式：60 = 2² × 3 × 5

关键点：

• 必须用质数试除,合数会重复分解（如用4试除会导致错误）。
• 遇到无法整除时,换下一个质数（如试除2后换3，而非跳过）。

快速判断质数的技巧

1. 观察尾数：偶数（除2）和末位为5的数（除5）一定不是质数。
2. 试除法：用小于等于√n的质数试除n，判断17是否为质数，只需试除2、3（因为√17≈4.12）。

常见错误与纠正

• 错误1：将1当作质数。
  纠正：1既不是质数也不是合数，分解时需排除。
• 错误2：分解不彻底，遗漏质因数。
  纠正：确保最后结果为1，所有因数均为质数。

实际应用场景

1. 约分：通过分解分子分母的质因数，快速找到公因数。
2. 解决几何问题：计算图形的最大边长或最小面积时，分解质因数可简化运算。