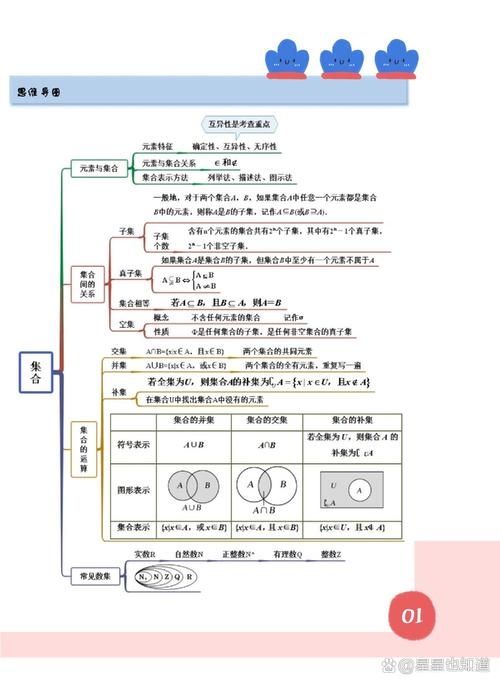
元素特性是核心
区分集合的关键在于明确元素的属性与关系,以数集为例,元素均为数字,如自然数集、整数集;点集则由坐标点构成,如平面直角坐标系中的点,若题目中出现“方程解的集合”,则属于解集,需通过求解方程确定具体元素。
三种方法快速判断集合类型
-
观察元素类型
- 数字、字母、符号 → 数集或离散集合
- 坐标点、几何图形 → 点集
- 方程/不等式的解 → 解集
-
分析元素关系
- 元素间有明确运算规则(如等差数列) → 规律性集合
- 元素满足特定条件(如x²<4) → 描述法集合
- 元素无序且互异 → 基本集合特性
-
注意描述方式
- 列举法({1,2,3}) → 元素有限且明确
- 描述法({x | x>0}) → 隐含条件需转化
- 图示法(韦恩图) → 强调集合间运算
易混淆点破解
- 区间与数集:区间是特殊的数集表示形式,强调连续性(如[1,5]包含实数)
- 空集与单元素集:空集无元素(∅),单元素集含唯一元素({0}≠∅)
- 点集与数集:点集元素为有序对(如(2,3)),数集为单个数
实战技巧
遇到复杂集合时,先提取元素再分类:
- 将文字描述转化为数学符号
- 判断元素是否满足“确定性、互异性、无序性”
- 用排除法剔除不符合项(如点集中混入单个数字)
个人观点
集合区分本质是逻辑分类训练,建议多做“逆向练习”:给定一个集合,尝试用三种不同方法表示它,例如将{x | x=2n, n∈N}转化为列举法或图形表示,这种多维度的理解能从根本上提升集合运算能力。(完)