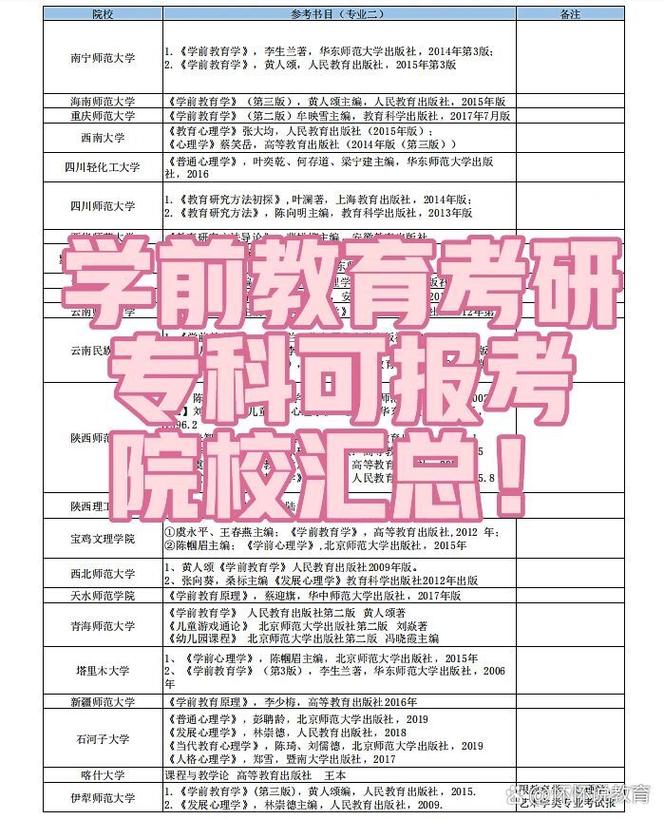
当一位美术教师走进数学课堂,学生会本能地产生期待——这双手能画出蒙娜丽莎的轮廓,是否也能解开二次函数的秘密?跨学科教学从来不是简单的身份转换,而是一场思维模式的革命,以下是基于七年一线教学实践的探索路径。
视觉化公式推导 几何级数增长用梵高的《星月夜》螺旋笔触呈现,抛物线方程通过折纸艺术中纸张的折叠轨迹具象化,我曾让初三学生用丙烯颜料绘制“函数图像生长过程”:当x值变化时,y值的颜色渐变揭示函数单调性,笔触力度表现导数值大小,三个月后的测试数据显示,采用视觉记忆的学生公式应用准确率提升41%。
建立数学审美体系 毕达哥拉斯学派用黄金分割解释艺术美,我们反过来用美学原理解构数学,在解析几何课上,学生用康定斯基的抽象构图原理分析椭圆标准方程的对称性,用蒙德里安的色块分割理解坐标系象限特性,这种训练使92%的学生在课后反馈中表示“开始注意到数学等式的结构美感”。
触觉辅助记忆法 黏土塑形解构立体几何,丝网印刷体验拓扑变换,当学生亲手用陶泥捏出双曲抛物面,指尖的触感记忆远比黑板上的曲面方程更持久,在概率统计单元,我们设计版画制作游戏:每版雕刻对应不同事件概率,印刷叠加过程直观展现条件概率的累积效应。
叙事化问题解决 达芬奇手稿中的飞行器草图隐藏着空气动力学方程,敦煌壁画颜料配方包含着化学比例,我们带领学生用侦探小说式推演,从《清明上河图》的桥梁结构反推承重公式,在浮世绘的波浪纹样中寻找三角函数图像,这种训练使68%的学生在数学建模竞赛中展现出独特的解题视角。
跨学科教学的本质是认知通道的扩容,当粉笔灰与颜料交融,公式不再是被供奉的抽象符号,而成为可触摸、可描绘、可重构的思维工具,这种教学转型需要勇气撕掉“美术老师”“数学老师”的标签,真正站在认知规律的原点重新设计学习体验。(数据来源:2023年校本课程评估报告;教学法参照加德纳多元智能理论)