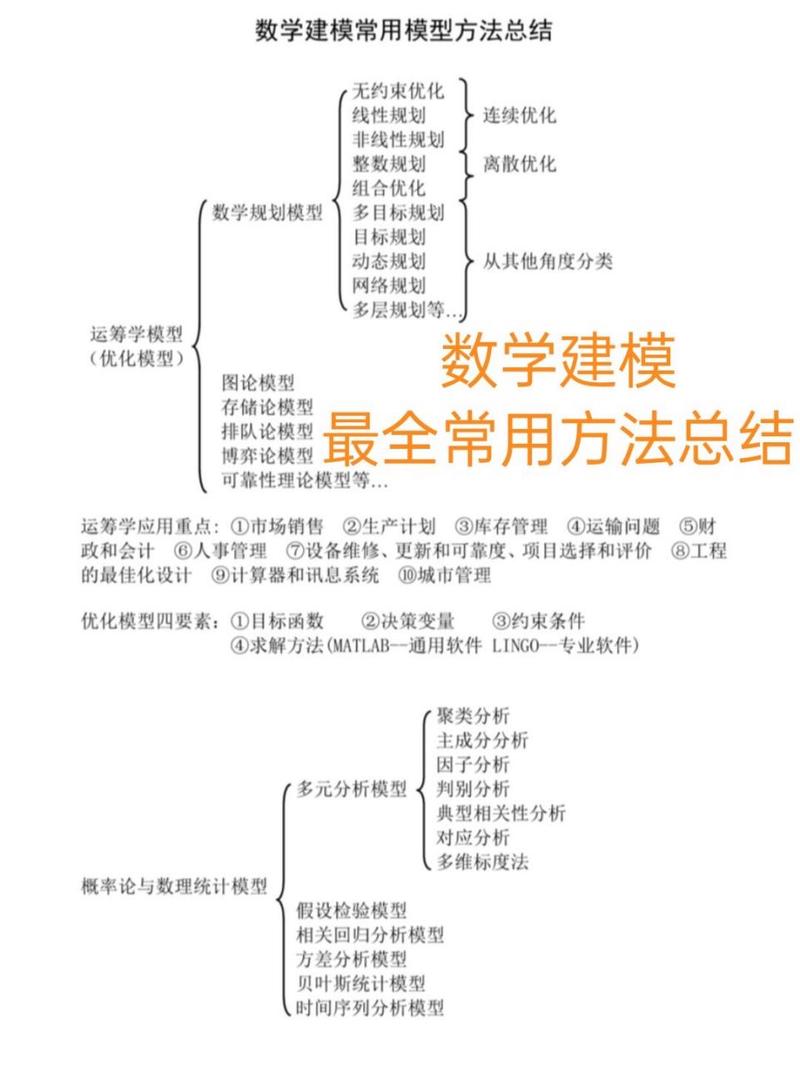
数学建模的核心步骤
- 精准定义问题 需求,剔除冗余信息,抓住核心矛盾,预测城市交通拥堵”需转化为“分析车流量、道路容量与信号灯策略的关系”。
- 合理提出假设
根据问题复杂度简化模型,如假设车辆匀速行驶、忽略突发事故影响,清晰的假设能缩小求解范围。 - 构建模型框架
选择数学工具:微分方程适合动态过程,图论适用于网络关系,统计模型擅长处理随机性数据,避免强行套用高级算法,适用性比复杂度更重要。 - 求解与验证
用MATLAB、Python或SPSS等工具求解后,必须通过敏感性分析(如调整参数观察结果波动)和实际数据回测验证模型可靠性。
90%新手踩过的三个坑
- 盲目追求复杂算法
用神经网络预测小型数据集,反而因过拟合失去泛化能力,建议优先采用线性回归、层次分析法等基础模型。 - 忽略模型解释性
若无法向非专业人士讲清模型逻辑,即使结果正确也可能被判定为“黑箱操作”,建议用流程图辅助说明各变量关系。 - 团队分工失衡
编程手独占建模、写手不参与讨论,会导致最终论文逻辑断裂,每日至少两次全员讨论,确保信息同步。
提升竞争力的实战技巧
- 建立工具箱意识
- 数据处理:Excel快速清洗,Python Pandas处理10万级以上数据
- 可视化:Tableau生成交互图表,Origin绘制学术级曲线
- 协同工具:Overleaf在线LaTeX编辑,GitHub版本管理
- 从经典案例逆向学习
研究全国赛获奖论文时,重点观察:
- 如何将“提高物流效率”转化为TSP问题
- 怎样用熵权法替代主观赋权
- 灵敏度分析部分的表述逻辑
- 刻意练习薄弱环节
统计显示,70%的建模失误源于数据预处理不当,可通过Kaggle数据集专项训练缺失值填充、异常值处理能力。
个人观点
数学建模的本质是“用数学讲故事”,评委和读者需要同时看到严谨的公式推导与清晰的实际意义,建议在论文摘要部分用“我们发现了X与Y的非线性关系,当Z>5时系统将发生相变”代替“我们建立了三个模型”,好的建模者应像桥梁工程师:一端深扎数学地基,另一端紧密连接现实世界。