,但很多同学刚接触时会觉得抽象,如何理解它?关键在于把数学概念与生活联系起来,用清晰的逻辑拆解问题,下面从三个角度切入,帮你掌握概率的核心方法。
从“可能性”到数学语言 生活中的“可能”“不一定”在数学中需要精确表达,比如天气预报说“明天降水概率70%”,意思是假设相同天气条件重复100次,大约有70次会下雨,概率范围永远在0到1之间——不可能事件概率为0(如太阳从西边升起),必然事件概率为1(如人呼吸需要氧气),特别注意:概率为1的事件未必绝对发生,比如在无限次试验中,概率1表示“几乎必然”。
计算概率的两把钥匙
-
古典概型:适用于结果有限且等可能的情况,比如抛硬币时,P(正面)=1/2,计算步骤:
- 列出所有等可能结果(如骰子有6个面)
- 找出目标事件的结果数(如点数为偶数的3种情况)
- 概率=目标结果数÷总结果数
-
频率估计:当结果不等可能或无法穷举时,通过大量重复试验计算频率,比如检测口罩合格率,抽检1000个有950个合格,则合格概率可估计为0.95,注意:试验次数越多,估计值越接近真实概率。
避开三大思维陷阱
-
错觉1:抛硬币连续5次正面,下次反面概率更大
纠正:每次抛掷独立,第6次正反面概率仍是1/2,历史结果不影响独立事件。 -
错觉2:“中奖概率1%”等于抽100次必中1次
真相:抽100次至少中1次的概率实际是1 - 0.99^100 ≈63%,这说明概率是长期趋势而非短期保证。 -
错觉3:所有概率问题都能直接套公式
实例:从3红球2白球中连续取两个(不放回),第二次取红球的概率?
错误解法:认为第一次结果影响第二次,复杂计算。
正确思路:由于每个球被取顺序机会均等,直接看作任取一个位置,P=3/5,这种对称思维能简化计算。
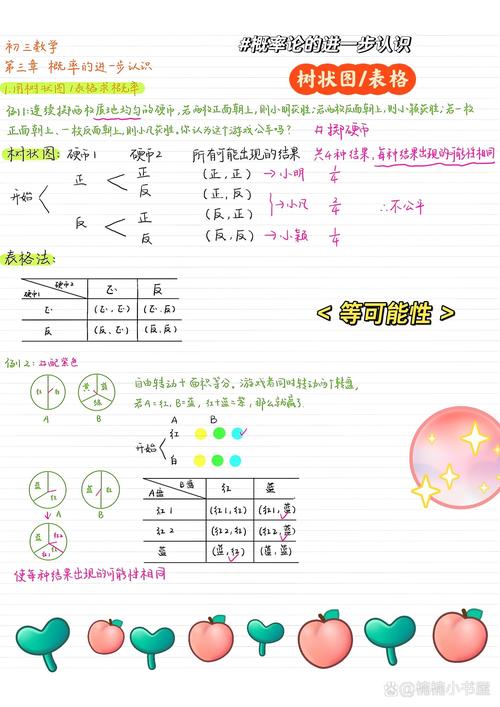
用工具让思考可视化 遇到多步骤事件,推荐两种方法:
- 树状图法:适合分步进行的实验,比如研究先抛硬币后掷骰子的组合概率,第一层画正反两支,每支再分6条骰子结果。
- 表格法:适用于两个变量的组合,比如比较两个骰子点数之和的概率分布,横向列第一个骰子结果,纵向列第二个,填满36格后统计各和出现次数。
概率学习最忌死记硬背,曾有个学生在商场发现抽奖转盘分区角度不同,立刻想到概率与圆心角成正比,这就是把知识用活的表现,建议多观察生活中的随机现象——体育比赛的胜负预测、游戏装备的爆率设定、交通信号灯的等待时间,背后都有概率原理,当你开始用概率眼光看世界,数学就不再是试卷上的分数,而是理解复杂世界的解码器。