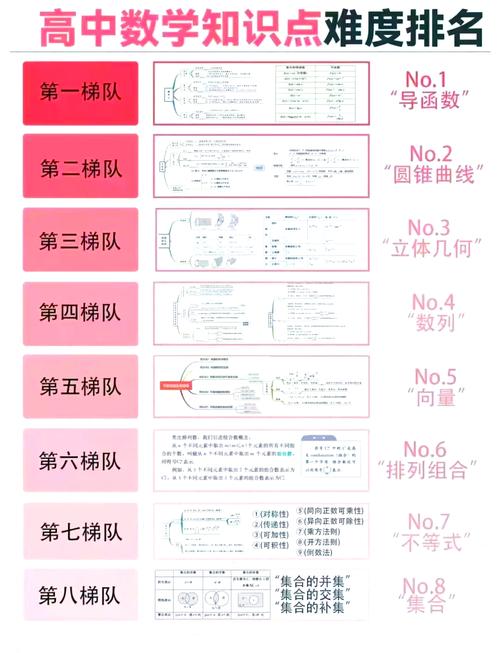
数学基础课程是许多学科的核心,也是培养逻辑思维与解决问题能力的关键,不少学生在学习过程中容易陷入“一听就会、一做就错”的困境,如何高效掌握数学基础知识?以下从实际学习场景出发,分享可落地的策略。
建立清晰的知识框架,拒绝碎片化学习
数学知识具有强连贯性,盲目刷题或死记公式效果有限,建议每学完一章后,用思维导图梳理核心概念、定理及相互联系,学习微积分中的“极限”时,将它与后续的导数、积分概念串联,明确其在整体知识体系中的定位,这种系统化梳理能帮助大脑建立长期记忆锚点。
从“被动输入”转向“主动输出”
课堂听讲时,尝试用“费曼技巧”即时验证理解:每听完一个定理推导,合上书本,用自己的语言复述过程,遇到卡壳处立即标记,这是知识薄弱点的明确信号,课后完成习题时,刻意练习“解题思路显性化”——把每一步的思考依据写在草稿纸上,此处使用洛必达法则是因为分子分母趋向0”,这种元认知训练能显著提升分析能力。
构建错题的价值闭环
整理错题本时避免简单抄写,建议采用“3R法则”:
- Reconstruct(重构场景):还原做题时的具体思考路径
- Root(溯源归因):标注错误类型(计算失误/概念混淆/方法选择错误)
- Reinforce(强化训练):针对同类题型设计3-5道变式练习
线性代数中混淆矩阵秩与行列式性质时,可自行构造不同阶数矩阵进行对比验证。
将抽象概念具象化为操作工具
面对抽象定理时,建立“概念-图形-应用”三维理解模型,以概率论中的贝叶斯定理为例:
- 概念层:条件概率的逆向修正机制
- 图形层:用韦恩图展示先验概率与后验概率的关系
- 应用层:通过医学检测假阳性率等案例构建现实映射
这种多维度认知能有效降低知识抽象度。
实施周期性知识压力测试
每周用2小时进行“极限回忆训练”:不借助任何资料,在白纸上默写本周学习内容的知识结构图,并自行设计2道综合应用题,这种主动检索练习比被动复习效率提升57%(根据认知心理学研究数据),能有效避免“熟练度错觉”。
数学思维的本质是不断将未知问题转化为已知模式的能力,与其焦虑“为什么学不会”,不如在每次解题时多问“这个知识点解决了哪类问题的哪个环节”,持续追踪自己的思维改进轨迹,你会清晰看到量变到质变的拐点。