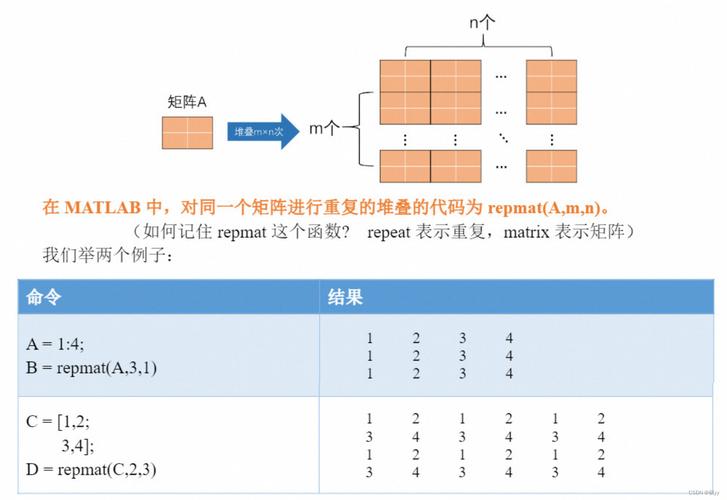
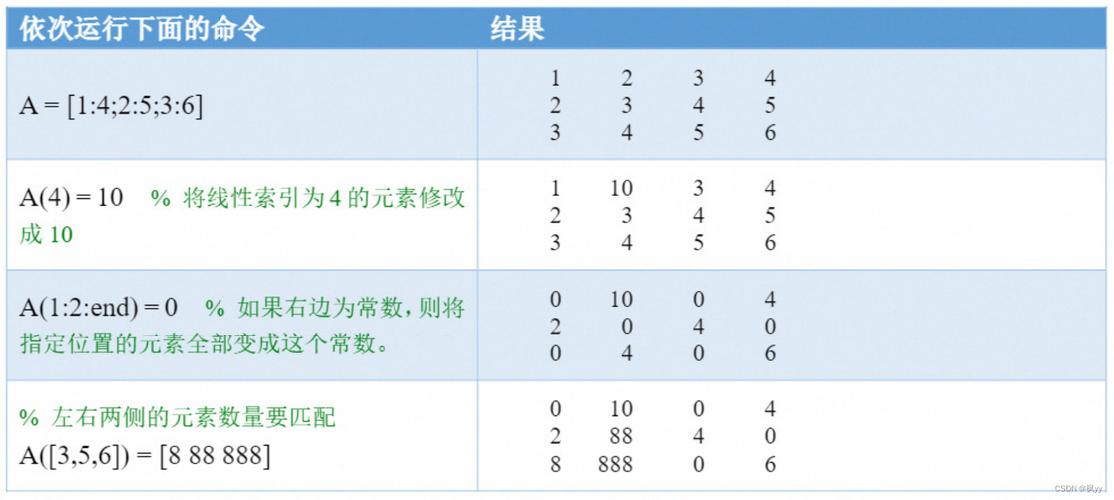
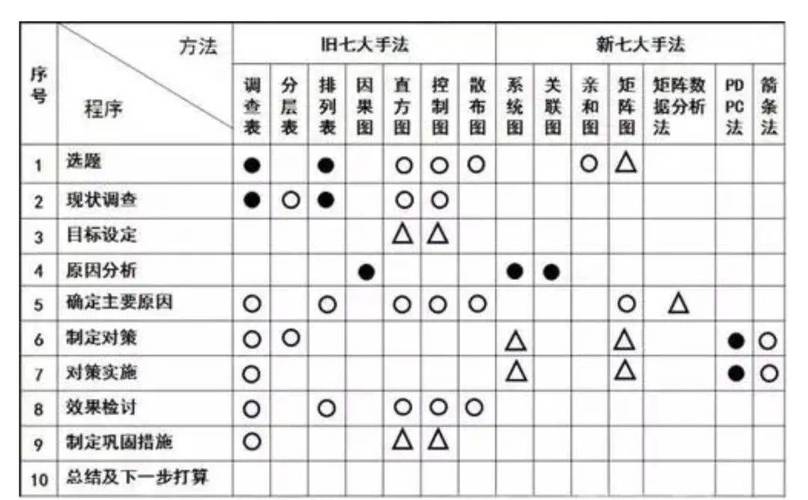
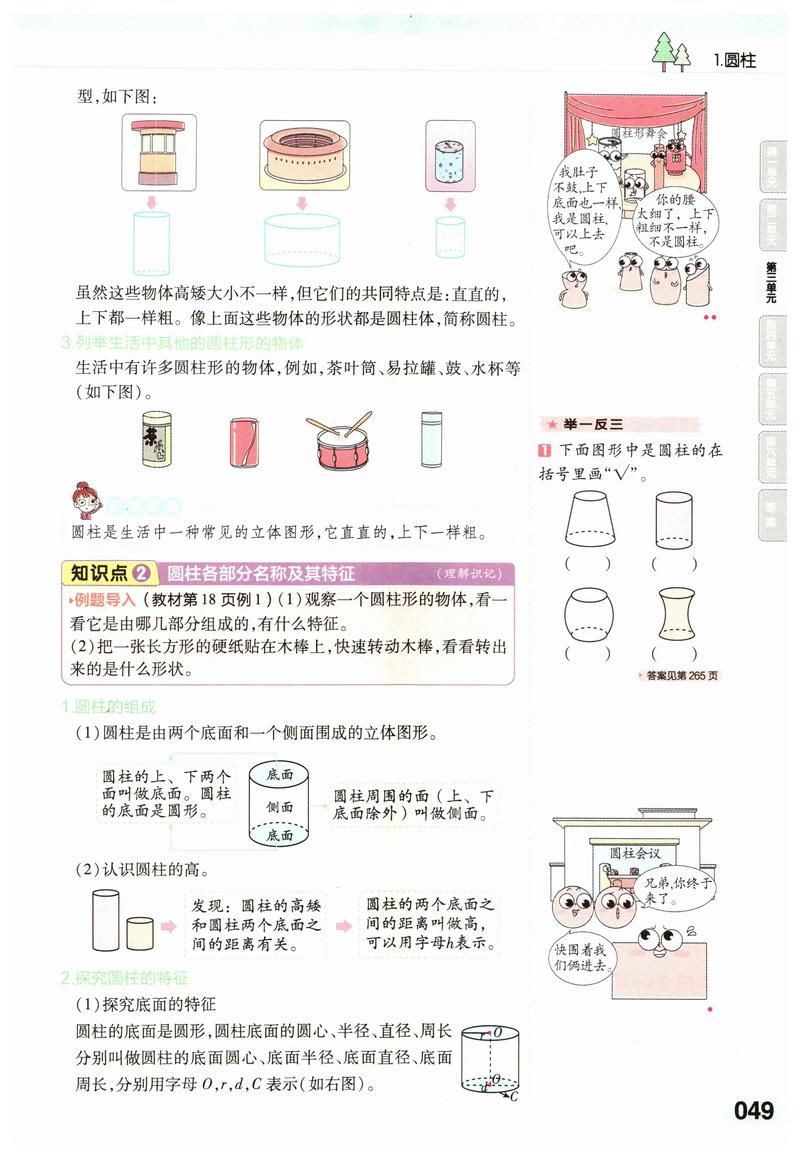
在数学建模过程中,矩阵是描述复杂系统、表达变量关系的重要工具,无论是线性方程组求解、数据降维分析,还是动态系统模拟,矩阵的构建直接影响模型的有效性和可操作性,以下是创建矩阵的实用方法及注意事项,帮助学生在数学建模中高效应用这一工具。
明确矩阵的核心作用
矩阵的本质是结构化数据容器,通过行与列的交叉点表达变量间的关联性,在交通流量模型中,矩阵的每个元素可能代表两个路口之间的车流量;在经济学投入产出分析中,矩阵可描述不同产业间的资源分配关系,构建矩阵前需明确三个问题:
- 矩阵需要承载哪些维度的数据?
- 行与列分别对应哪些具体对象或变量?
- 元素值的数学含义是什么(如权重、概率、数量)?
矩阵构建的典型场景与步骤
- 邻接矩阵(图论模型)
- 确定图的顶点数量n
- 创建n×n零矩阵
- 若顶点i与j存在连接,则A[i][j]赋值为边权(无向图需同步赋值A[j][i])
- 应用场景:社交网络关系分析、电路拓扑结构
- 系数矩阵(方程组求解)
- 将方程组标准化为AX=B形式
- 每个方程按变量顺序提取系数
- 缺失变量自动补零系数
- 示例:方程组
2x + 3y = 7
4y - z = 1
对应矩阵:[[2,3,0],[0,4,-1]]
- 特征矩阵(机器学习)
- 每行代表一个样本数据
- 每列对应一个特征维度
- 数据标准化处理(归一化、空值填补)
- 注意特征间的量纲统一
实用工具与校验技巧
- 编程实现(Python示例)
import numpy as np # 创建3×3零矩阵 matrix_zero = np.zeros((3,3)) # 从列表生成矩阵 data = [[1,2,3], [4,5,6]] matrix_custom = np.array(data)
- 可视化校验
- 使用热力图观察数值分布
- 检查矩阵是否对称(适用于特定场景)
- 验证行列式值是否合理(如协方差矩阵需半正定)
- 常见错误规避
- 维度不匹配时拒绝运算(如3×2矩阵与4×1向量相乘)
- 稀疏矩阵优先使用压缩存储(CSR/CSC格式)
- 动态模型注意矩阵的时变性标记
矩阵优化的进阶策略
当矩阵规模超过100×100时,传统遍历方法效率显著下降,建议采用分块矩阵处理技术,将大矩阵分解为若干子矩阵并行计算,例如在环境扩散模型中,将区域划分为网格子块,分别建立污染物浓度子矩阵,再通过边界条件进行矩阵拼接,合理利用矩阵的稀疏性特征,能减少80%以上的存储空间占用。
数学建模的本质是将现实问题转化为可计算的数学结构,而矩阵正是实现这种转化的桥梁,建议重点掌握Numpy、MATLAB等工具的矩阵操作函数库,并在建模过程中养成“先设计矩阵结构,再填充具体数据”的思维习惯,遇到复杂系统时,尝试用矩阵分解(如SVD、LU分解)揭示隐藏的系统特征——这往往是突破模型瓶颈的关键。