九年级几何题中如何有效运用辅助线解题？

几何题找不到思路？辅助线是解题的“金钥匙”，但很多同学要么不敢画，要么乱画，导致题目越做越复杂，今天结合九年级高频考点，分享辅助线的实战技巧,看完直接上手用。

中点相关辅助线：构造对称与全等 遇到线段中点,优先考虑以下两种方法：

1. 倍长中线法：延长中线使延长段等于原中线，构造全等三角形
   例：△ABC中AD为中线，延长AD至E使DE=AD，连接BE，可证△ADC≌△EDB
2. 连接中点构造中位线：出现多个中点时，连接形成中位线
   例：梯形ABCD中，E、F为腰AD、BC中点，连接EF，则EF=½(AB+CD)

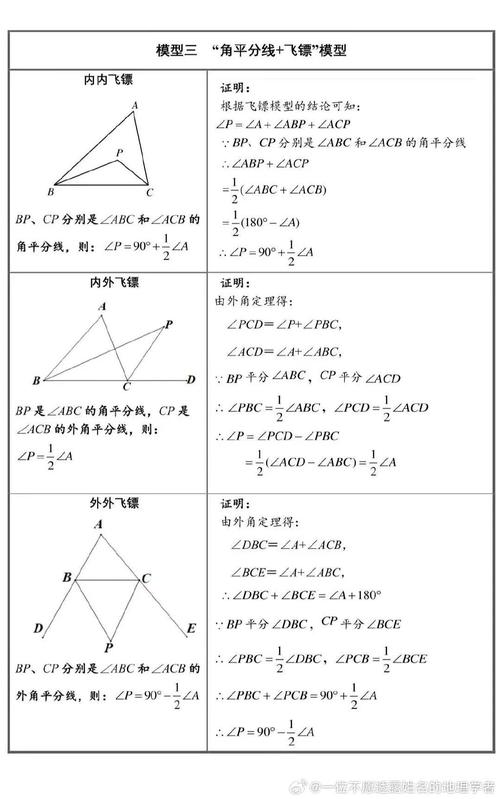
角平分线辅助线：作垂线or对称轴 看到角平分线,立即想到两种处理方式：

1. 向两边作垂线：过平分线上点作两边的垂线段，长度相等
   实战：证明角平分线定理时，过D作DE⊥AB，DF⊥AC，必有DE=DF
2. 构造对称图形：以平分线为对称轴翻折图形
   技巧：在证明线段和差关系时特别有效，例如截长补短法的应用

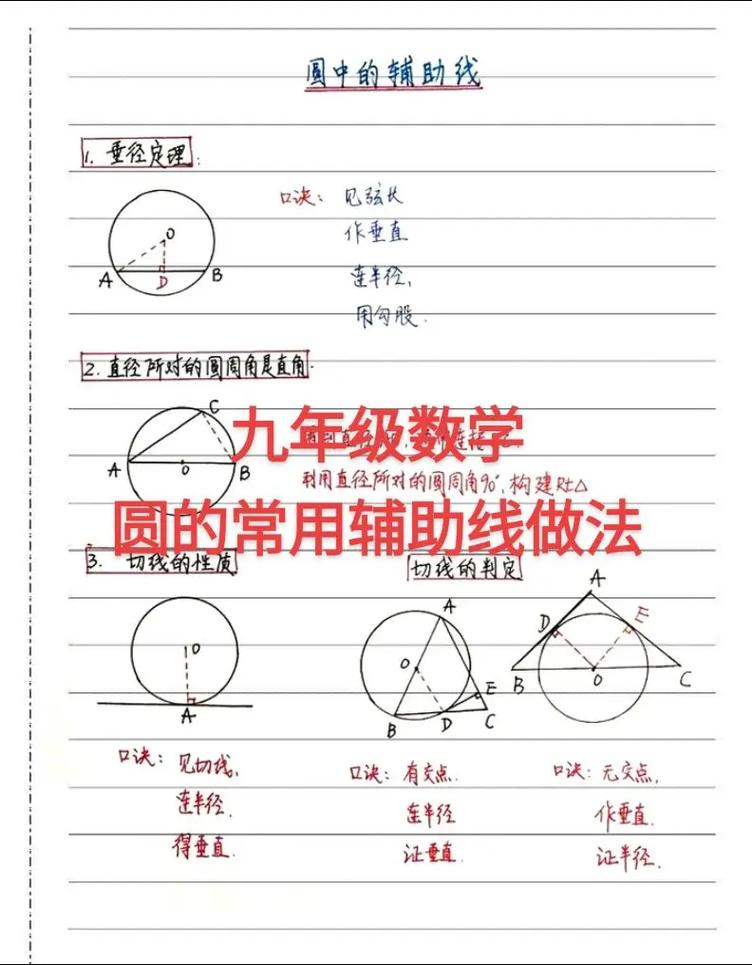
圆相关辅助线：五大必会套路

1. 见切线连半径：立即连接切点与圆心，得到直角关系
   注意：若题目说"切线长"，记得用切线长定理
2. 相交圆连公共弦：两圆相交必连公共弦，方便找角关系
3. 直径所对圆周角：出现直径马上标注直角符号
4. 弦中点连圆心：出现弦的中点，必连圆心构成垂直关系
5. 构造辅助圆：当四点共圆条件不明显时，主动构造辅助圆解题

特殊角度处理法 遇到30°、45°、60°等特殊角时：

1. 构造直角三角形：特别是含30°的情况，可补形成30-60-90三角形
2. 等边三角形转化：60°角附近构造等边三角形，利用三边相等特性
3. 正方形辅助线：45°角可考虑构造正方形或等腰直角三角形

动态思维训练 真正的高手画辅助线不是记套路,而是有清晰的逻辑链：

1. 逆向分析法：从结论反推需要证明什么条件
2. 条件关联法：把题目中分散的条件用辅助线串联
3. 模型匹配法：识别题目中的基本模型（如手拉手模型、半角模型）

建议准备专门的辅助线练习本，把做过的经典题按类型归类，每次画辅助线时用红笔标注思考过程，三个月后再看这些标注，你会发现自己的思维盲点，辅助线从来不是玄学，而是有迹可循的逻辑推导——这个观点,我在带过的12届毕业班学生身上反复验证过。